Ensign Rod index

Years ago, i wrote a seven part set of very short related stories. Part zero was rejected. The publisher wanted action, not set up. Part one was published to a collection of these stories. Later, this collection was dropped from the Internet. The goal was about 1,000 characters per story. My goal was to get as much plot as i could in that short space. I hadn't yet read any of Kathy's helpful Slash the Word Count hints. https://kathysteinemann.com/Musings/word-count-main/ 
Please enjoy Ensign Rod, the micro-story.

https://predelusional.blogspot.com/2008/06/rod-part-zero-of-six.html
https://predelusional.blogspot.com/2008/06/rod-part-one-of-six-battle.html
https://predelusional.blogspot.com/2008/06/rod-part-two-of-six-adrift.html
https://predelusional.blogspot.com/2008/06/rod-part-three-of-six-winders.html
https://predelusional.blogspot.com/2008/06/rod-part-four-of-six-historian.html
https://predelusional.blogspot.com/2008/06/rod-part-five-of-six-its-tie.html
https://predelusional.blogspot.com/2008/06/rod-part-six-of-six-coffee.html

The golang tutorials

 I started learning Google's computer language "go" (also called golang, likely due to how easy it is to search for "go" in Google) about three years ago. I run Linux, so I downloaded "go" and started the tutorials. I think i got pretty far into it because i wrote a couple of the benchmarks i've written in other languages: c, fortran, perl, java, guile (scheme), php. These are the matrix multiply and the prime number sieve. It took a while, but i found the "go" sources on my system. They even work.

However, i had upgraded my Linux operating system to Linux Mint 19 (Mint is derived from Ubuntu, which is derived from Debian). I needed "go" again, so i installed it from the repository. Really easy. I got go version 1.10. The current version is 1.16.

I started the tutorials again, thinking i'd breeze through them, just as a refresher. However, bits from the tutorial stopped working pretty quickly. I did a bunch of Google searches. Frankly, it was frustrating. Eventually, concentrating on this one problem all day, i stumbled across something that suggested that the command "go mod tidy" was introduced in go version 1.14. I told the Linux package manager to remove go, downloaded the version 1.16 tarball and installed it.

That's what i get for trying to learn a new fast changing language. Hopefully, i'll use it often enough that i won't have to go through the tutorial again. At least my benchmarks still work.

JOKER

One of the things i'd like to find out from a movie review is if i'll like the movie, but if at all possible, without learning the entire plot with nuances. And that's what is attempted here with Joker.

https://www.imdb.com/title/tt7286456/

Let me be clear. There's a pandemic, so i'm not saying you should go out and see this. I'm also not saying you should rent it or stream it. Be safe. But read on to see if you're wasting your time/money.

The 2019 movie, Joker, is an origin story for the (primarily) DC's Batman villain - The Joker. As a comics fan, i'm generally disappointed in movies that do origin stories. As a classic example, Marvel Comic's Spider-Man suffers no less than three quick origin movies, two which are minor changes from the original comics origin, and the third which resets Spider-Man's character who should be about 60 years old now to some time in high school, with no rhyme or reason. That Marvel's characters generally age adds realism to their characters. That Marvel sometimes loses control and by default allows a rehash of the same story repeatedly is disappointing.

The Batman character's story has changed dramatically in various iterations. The 60's TV Batman played by Adam West is a campy show that doesn't take itself too seriously, whereas the Dark Knight gets "why so serious?", from the villain, The Joker. Is this the same Joker as in this 2019 movie? Maybe. That the Dark Knight is so different suggests an excuse for the Batman Begins origin. Fortunately, that movie also has what the new Batman ends up doing, facing a villain, character growth, and so on. Not bad.

You'll like Joker if realism is your thing. And yet, it's easy to imagine that a Joker story could venture into horror, with attendant paranormal activity. But there's none of that here. Joker's insanity is based on real mental conditions. The only horror sort of activity is that it's not at all clear what he's going to do next. In fact, it's not always clear if what has been shown is what the character actually did or what the character imagined. The plot is so good, script is so good, the acting is so good, the photography is so good, the situations are so good, that the result may be a little too close to home for many. Maybe you know someone with a similar diagnosis.

It turns out that i liked it. Here's what i liked about it. With an origin with this kind of depth and realism, it should be easier to write additional excellent stories. It should be easy to add incidents to the base origin that are compatible with the existing story, and hints of these can be added to ongoing encounters with the hero or heros. The hero learns about the character and takes it into account, allowing the hero to be more heroic, and, for example, not simply a guy who spends his nights beating up people with his bare hands. The hero has goals. The villain has goals. They both need to have some complexity if your going to have very many stories with them.

Resume

I've never rejected anyone on the basis of their resume.

First, especially my early resumes were retyped by the agency, and all sorts of typos were introduced, especially in acronyms. I'd be in an interview, and they'd ask me what one of these means. I've never seen this resume. Often, when i'd told them stories about what the resume was supposed to say and what the job was really about, they made me an offer.

Second, only about one in three candidates actually show up for their interviews. After about ten who actually show up, we get someone who's English is so bad, we can't tell if they know what they're doing or not, even after talking for an hour. I'm thinking (optimistically) that this is someone i could train. We get together and decide that this would, in  fact, be someone we'd have to talk to from time to time, and a rejection is made.

We finally get a competent candidate who accepts our offer. They show up and start working, but they go out to lunch and never return. I'm starting to think that the job wasn't so hot either.

Popups

I've been looking for stuff on the Internet. Gasp. Using a search engine. I'm going to many, many sites i don't usually go to. A ton of them have this annoying and pointless behavior. As the page is loading, i start reading it. I get about two sentences, tops into it. At that point, the entire content of the page is blocked by a popup. Is it an ad? Not exactly. It's a "click here to subscribe to our email list" or some equivalent. But two sentences into their content is not nearly enough for me to decide if it's at all interesting. So this is pointless. By the time i finish reading the content, i should have a better view on it. If i don't get there, the answer is likely "no" anyway. So, why not have a form, not in a popup, but at the bottom of the page, on the page itself? That's the right time. I won't have to dismiss it if i don't want to sign up. Don't get me wrong. I like spam. At least, i like spam if it's the kind of spam i like.

Steven Pinker and the Ivy League School

I nearly didn't read this article, because i haven't read Deresiewicz’s article. And, Deresiewicz’s article doesn't sound like a good use of time. I also haven't seen the movie Love Story, probably for the same reason that i haven't watched Titanic, despite owning a copy (not entirely my fault). But i may have to watch Love Story, since the wiki plot synopsis doesn't seem to have enlightened me enough. I'm likely missing details of the plot.

But, it's a good article. I'm glad i read it. And, it matches my experience working for four Universities, which includes Harvard, two state schools, and a selective university (i have additional experience at another selective university and a state school, and they match prior experience, more or less). Yes, i admit, i don't really want to spend time reading an article that doesn't support my biases.

I could have applied to go to Harvard. I considered MIT enough to order a course catalog. But they didn't look like a good deal, in fact, they seemed to offer less than the state school, and in ways consistent with this article. It seemed obvious, but in retrospect i spent great gobs of time on it. At the time, MIT was considered a great graduate school.

The "teach you how to think" line was in vogue where i went to school. No one seemed to have any idea how to do it, or measure the effectiveness of any ideas that might come up. That seems to be changing. But in any case, they did, for the most part, make an attempt to teach stuff one might need. And above all, they came up with a way to get the students to demonstrate competence. This last bit is important. Most schools don't do this (I'm not aware of another that does). And yet, it's why i went to school.

I love this: "Perhaps I am emblematic of everything that is wrong with elite American education, but I have no idea how to get my students to build a self or become a soul." Not many would have the courage to say something like that. But the emperor doesn't have any clothes. And it turns out that courage is something that is important for both student and teacher to have. Perhaps it should be taught. In any case, it should be easier than teaching "building a self".

His list of stuff students should learn is very good. Perhaps it should start in middle school, dumbing down nothing, and including the bits under "a liberal education". And the goals should be introduced even earlier. The idea that i'd ever "appreciate that people who disagree with me are not stupid or evil" is going to be hard to swallow. I've seen people who are obviously evil who act like they're stupid. While i try not to go off the deep end on conspiracy theories, Watergate really did happen. And, i think, the goal is in conflict with knowing how to distinguish vetted fact from superstition, etc.

At the end of the article there is a conclusion. Should Harvard adopt merit based admissions? Perhaps they could do it as a pilot project. Perhaps they've already got pilot project statistics, and they could go with the results. Perhaps they could look to see if someone else has already done this experiment, and go with the results. In summary, these ideas are Run an experiment, look at data you already have, and learn from others. As these are skills that Harvard should be teaching their students, perhaps they could simply turn these ideas into student projects, then evaluate the projects and use the results.

Management and The Art of War

In Sun Tzu's The Art Of War, one of the lessons is that a good strategy involves teaching your staff good tactics, then using the good tactics to advantage. So, today's Harvard B school management, with its emphasis on how much money is made each quarter, and stupid slogans totally misses the point. Following this plan dooms your business to slow death. Toyota seems to have noticed this. Toyota replaces robots with humans. this problem is not confined to the automotive industry.

Readers of this blog may have noticed that there is a bias towards education. So, let's say that you're a leader of a major organization, involving multiple technologies. How do you educate your staff? You could simply hire college graduates. But the pool of graduates is getting smaller. College costs too much except for those lucky enough to be born into wealth. The middle class is becoming part of the poor. It's not enough. And besides, college doesn't teach people how to make your business work. They still need to learn that on the job. Who do they learn it from? Well, they need to learn it from people already doing the job. But doing this means that your business will tend to simply learn how the business operates, not how it should operate. You can get some more input from contractors. After all, these people very likely have worked for your competition. And even if they aren’t currently as good as you are, they have something to teach you, even if it is by obvious bad example. Contractors are currently treated as second class staff. This is not the way to build a smoothly working organization. It’s a way to alienate part of your staff. It was my opinion that engineers should spend at least some of their time on the factory floor figuring out how to make things work easier, faster and safer. And by engineers, i mean everyone who could learn something for the organization.

In order to create strategy that incorporates good tactics, management must learn all the best tactics. But even if the CEO is already an engineer, that doesn't mean (s)he knows all kinds of engineering, or computer science, or networking, or communications security, or telephony, or building design, or logistics, or finances, or marketing and so on. How does one do it? Well, IMO, the CEO should have depth in at least something, but likely many such things. But also, the CEO should have a skills team covering all bases that can provide advice. And the CEO has to know the language of all the skill team members so that the advice can be evaluated. I'm not saying that the CEO should micromanage the whole system. I'm saying that the CEO should be able to build and tune strategy that allows the whole company to work efficiently. One of the things that management of larger companies currently does is build fiefdoms or silos that insulate groups from different disciplines making communication and cooperation between groups slow, difficult, unresponsive and otherwise dysfunctional. These structures build in inflexibility, and one hears "that's not the way we've always done things" (a phrase that is nearly always something that is demonstrably a lie).

Edmunds on fuel economy

Edmunds has done a fairly complete set of tests of fuel economy in a sort of Myth Busters way. They mostly match my own results.

I use cruise control aggressively, if i have it. That is, i use if even if it only marginally makes sense. That's because it gives me 4% to 5% fuel economy at the same speed. And, it generally reduces my workload.

I consistently get 17% better fuel economy for going 62 MPH rather than 70 MPH. Why 70? Michigan's highest speed limit is 70. I try very hard to not speed. Why 62 MPH? My speedometer also shows KPH, so there's a handy reference - 100 KPH. Naturally, Edmunds gets a higher percent improvement. Often overlooked is that driving slower is safer. We tend to increase our risk to some threshold. I try to minimize my risk unless there's some corresponding benefit. Usually there isn't.

Drafting: I've tried drafting manually. I found that drafting a truck fairly got me worse fuel economy than driving at the same speed. And, driving at the same speed with cruise control is better yet. Drafting is risky, and pointless, so i don't do it. This test was done on a cross country trip, covering about 400 miles each. Wind and terrain were similar. My guess is this. Constant speed changes, through brakes or engine drag, kill fuel economy. Engine drag is the same as the brakes.

Roof luggage. I lost between 5% and 10% for putting roof luggage on my car. Cruise control was used at the same speed on the same course for thousands of miles. My luggage carrier at least looks fairly aerodynamically efficient. The way i look at it is that you put roof luggage up there if you need it. I'd love to be able to drag a trailer. It would be better than driving a pickup and paying the cost all the time.

A/C. I've not done this test. I'm not into noise, so i don't drive with the windows open on the highway. I've read articles about just this topic. The answer seems to depend on the details; such has speed, the kind of car, and so on. It's not a huge difference anyway.

Tire pressure. I underinflated the tires on my car. It did not change my fuel economy in any measureable way. I overinflated my tires, and again, no change. But i view it as a safety issue. For at least one of my historic cars over inflation leads to over steering.

Manual transmissions. I've heard otherwise, but my tests show that manual transmissions save you at least 5% in fuel economy over automatics. I'm not a gear head who likes to shift gears. What i'd like is a series hybrid. That is, and electric transmission. With no differential, we'd get an additional 7% to 15%. With no engine drag, we might get another 20%. There shouldn't have to be any gears, so there's smooth acceleration always. It should last longer than hydromechanical automatic transmissions. It should have redundancy that will get you home even if a wheel can't be powered. It should be cheaper to replace if it does fail.

My conclusions match too. The main issue is psychological. I used to have an hour commute to work. Driving faster could save me, at most, about five minutes. But since there were traffic slowdowns, it was impossible to measure five minutes. Psychologically, it's difficult to let everyone pass you. This is the biggest hurdle. But i can use the cruise control much more often at 62 MPH than at even 65 MPH. Everyone else has to pass me. I have the right of way. It's worth something.

Edmunds fuel economy tests

technology

I have a land line for a phone. I often get messages on my answering machine where the automated message machine gets the complete message onto my answering machine. Today i got "Press 2". That's an entire message. I also got "Press star now to repeat this message". These were different voices, so presumably, different senders. Total fail.

For a list of the ways that technology has failed to improve our lives, please press 1.

Caffeine: last part with any luck

Last May, my left shoulder started hurting really bad. I recognized the symptoms. I had them in 2001, though in my right shoulder. Back then, i noticed that it didn't hurt quite so much on Sunday, especially Sunday afternoon. What did i know about Sunday? Well, that's when i'd get a headache from caffeine withdrawal if i'd had too much that week.

I never acquired the taste for coffee, but i can drink Mt. Dew in the morning. Mt. Dew is also an acquired taste, especially in the morning. It's not as vile as beer in the morning, though pretty close. I'd get withdrawal headaches on Sunday because i don't drink soda at home, just at work. So, the obvious experiment was to switch to Sprite, which has no caffeine. After two weeks, there were two things that were obvious. First, there was a clear connection. My shoulder pain had backed off considerably. I still had restricted motion. But it wasn't getting worse.

The second observation was unexpected. It turns out that i don't really like Sprite. So, i switched to water, and i ended up consuming about a half-gallon every day. A side effect of this switch was that i lost 37 pounds (17 kg). That's because water has about 700 fewer calories than Sprite or Mt. Dew in the quantities i consume. This lost weight wasn't hard to find. I don't remember, maybe it was under the bed.

In any case, this started in February 2001. Just in case i wasn't convinced, in March 2001, i went on a job interview. They offered me a cup of coffee. Again, i don't drink coffee. But on interviews, i seem to lose about 50 IQ points. It's amazing i ever get hired. It was one of those small Styrofoam cups. I drank it. My shoulder hurt like hell for four days. I still reach for things with my left hand, even though now that's the shoulder that hurts. The pain held pretty steady until the month of October. Then the pain ramped down to zero, and my restricted motion became unrestricted. But fast forward to now. This is month nine. Every day, my left shoulder's pain noticeably decreases and the range of motion increases. I fully expect to be totally cured by month’s end. That is, if i don't fall off the wagon. It really hurts to fall off the wagon.

Engines Under Ursus, SciFi podcast review

I've been listening to Engines Under Ursus, by Marin Brady. I've just finished the 26 episodes i had downloaded. There are at least two more. But my ancient 32 bit computer died, more or less. That's another story. This more modern machine i'm using is in a sort of zombie mode, booted from thumb drive, while it gets a brain transplant. Apparently, Marin has written a bunch of short stories. He says he wrote Engines, sent it to Tor, and got something unintelligible back. I don't usually write reviews before i've finished them, but this is an exception. If Tor rejected this piece, it's a mistake on their part.

I've heard Scott Sigler's audio for Ancestor, Infection (now called Infected), Earth Core, and The Rookie. I mention this for two reasons. First, i've had ear buds in my ears for about ten years now. And second, to compare experiences. Scott has great stories, uses voices for the parts, has some quirky reading. I couldn't get over how he'd mispronounce words sometimes. Easy words. He wrote the book, and the words are used right, but...

Martin Brady has some sort of accent. Maybe it's Irish. Whatever. He has multiple voices, and many don't have an Irish accent. They're quite consistent. While many actors, including voice actors, over act, Martin has a more subdued underacting style. It's not a monotone. I can only call it deliberate. And he takes the performance an extra step. He adds pod-safe music to each episode. The music is typically at the end of the episode. Frankly, i wasn't much interested in it. That is, until episode 19. I no longer have two hours of driving commute per day. So it's more unusual now to drive while listening. But for episode 19, i was. And i listened to the music because i didn't want to fiddle with the mp3 player. Holy shit. I practically had a nose bleed, it was so good. I don't even get nose bleeds. And there are lines and bits from the song that are in the episode. So now, i need to go back and listen to everything. So, while Scott moved the field forward by using audio books to get the word out (and it seems to be at least part of what's really working for him), Martin has added a dimension to audio story telling. The audio version is going to be, in my opinion, better than the printed version. I've had to go back and listen to the song, uhm, repeatedly. Apparently, Rockbox (open source firmware for my Sansa and other mp3 players) has a feature called "bookmarks". I figured out how to use them, and it has let me conveniently play this piece at will. I really hope Martin has high quality wav files so that his finished product can be released in higher quality mp3s, OGG, or FLACC files eventually. The piece deserves it. I'd buy it.

What about the story? Well, at first, i had no idea what to make of it. I mean for at least ten or fifteen episodes. For some books, at this point i'd stall, and either drop it, or pick it up later, often years later. But this was different. It was something like the movie Brazil (my favorite movie, BTW). Engines seems to be going somewhere. But in Brazil, even after watching the movie several times, and reading the screen play, i still have no idea where it's going, or for that matter, what happened. There's an unpredictability in Engines that i like. When i finished episode 26, i noticed that episodes 24 and 26 were on my player. Rockbox has a feature where you can delete a track before you've finished listening to it, if you're near the end. I must have listened to episode 25 out of order. I think it was in the low 20's. I recall wondering what Martin was up to. Martin wasn't up to anything. Sometimes authors move stuff around. But here, i did it, and it didn't matter as much as you'd expect. The story isn't over, but it's looking like a real winner.

Ursus is a planet other than Earth. There are aliens. Humans are aliens elsewhere. There are androids, and lots of tech stuff. It's not hard science fiction. But the science rules broken wouldn't completely change the story if they weren't, at least not so far. The story is about the story. I'd say more, but at this point, you should have all you need to decide if you want to read it. I wouldn't have written this review if i didn't like it.

What's your biggest weakness?

Interviewer: What is your biggest weakness?
Candidate: I'm too honest.
Interviewer: I don't think that's a weakness.
Candidate: I don't care what you think.

For the most part, i don't like most interview questions. Interview quizzes are terrible. A good question i heard in an interview was this:

What are your favorite tools?

This question draws out anecdotes and situations. The tools show diversity of activity, passion for the job, and can be genuinely informative. It can start a conversation. You don't really want a monologue. It can get you close to what should really happen in an interview. If the interviewer isn't competent, then the interviewer can't tell if the candidate is competent. The best interviews happen between two competent people. At the end of the interview, interviewers must ask themself this question: "Would I like to hang out with this person." Studies show that many companies have pockets of really good employees.
I said that i don't like most interview questions. I come away thinking, "How could they be so stupid?" (And, "do i really want to work there?") But for a long time, i wondered what the interviewer should ask. I give them (and myself) a bit of a break now.

It takes about two weeks to come up with a really good extemporaneous comment. -- Mark Twain

Sam was a pretty smart dude. If it took him two weeks, then we all deserve a break.

Passwords

I recommend making up a sentence. Start from a movie or book. Summarize an idea. Then maybe substitute a number for a letter. o, q => 0, i, l =>1, 4 => #, or whatever. Let's say you want to make up an 8 character password. You saw the first movie Thor. An original quote is this:

"Whosoever holds this hammer, if he be worthy, shall possess the power of Thor."

That's 14 words. Maybe "The worthy holding this hammer have the power of Thor". That's 10. Maybe "The power of Thor to the worthy". That's 7. But you heard it in the first movie. So add a 1. It's 1, so jam it in at the beginning. 1tpotttw. Of course, don't use this example. Use "The Password Of Thor To The Worthy One" instead.

So, you have to change passwords every month. And you can't remember which of your passwords is current. You could write "Thor" on a Post It note, and put it on your monitor. You can keep a running list of all your recent passwords on your monitor, in case you failed to change one of them. You've seen other movies, right?

lastpass.com

I'm not a troglodyte. I've used a password manager. Can you say "Single point of failure"? Many companies have password length restrictions, adding together the restrictions of numerous operating systems.

I wrote a password generator once. It tried hard to make up memorable passwords. They weren't that memorable. And, it turned out that it used the date/time to the second as a random number seed. What could go wrong? Well, if one can guess when a password might have been generated to within a year, that's only about 31,536,000 passwords to check. That's nothing for a computer.

Fire or Ice

The question was When is the end of the world?

Robert Frost had it right.

In five billion years or so, the Sun will grow into a Red Giant. Its diameter will be about the size of the Earth's orbit. Earth either is engulfed and vaporized, or raises a tide behind itself on the Sun, which removes orbital energy from the Earth, causing it to spiral into the sun, where it is engulfed and vaporized.

However, we're here. We already understand physics enough to know how to move the Earth's orbit out from the Sun. Essentially we steal orbital energy from Jupiter using big asteroid flybys of both planets. At this point, it's an engineering project. A big engineering project that takes millions of years. However, it's feasible, and would be worth doing. After the Sun's Red Giant phase, it shrinks to about the size of the Earth, and though it's really hot, its much smaller size means that it emits less total energy. We reverse the process, and move the Earth into a much smaller orbit for maximum comfort. Eventually the Sun cools. The Earth freezes. But it's ten billion years later, at least.

Robert Frost's Fire and Ice poem says it might happen either way. In his The Road Not Taken poem, he says "Two roads diverged in a yellow wood". The way that the Earth ends is our choice. Fire or Ice. Which do you want?

A moving experience

When i was in high school, one of my class mates said that he'd only been out of town once. That's when he was born. And that's because the town has no hospital. At the time, the idea that moving is anathema was a new idea. I didn't understand it. But it's much more common than my own history. I've moved 17 times since college. In fact, you can trace the movement of humans out of Africa and out the coast of India by using DNA. You call it movement, or migration. But it is really expansion. The descendants of people who moved out of Africa maybe fifty or seventy thousand years ago are still there. You sample their DNA to find out how long ago it was. How many generations stayed where they were for that long? Then we have a story like this:

A moving experience.

Something odd

What if we discovered something odd by accident. If boys between the ages of 9 and 13 are starved (not to death, just reduced food intake), then not only do they do better, but so do their children (if any) and their grandchildren (if any).... In fact, three generations have one quarter the chance of death by heart attack. And, what if we had a single payer health system (like Austrailia), so that effectively, everyone pays for health issues, not just the victim. And, let's say that heart attacks are painful to have, and incredibly expensive to treat. Wouldn't it make sense to starve boys between the ages of 9 and 13? Wouldn't it be the ethical imperitive? How would one go about explaining it to Americans?

Is there anything to this? Here's the podcast.Radiolab

Movies

I read this bit about ants and immediately thought of how people pick movies.

Movies are a great example. People see the trailers, and either watch or not. The first people who see the real movie talk about it. But movie promoters talk up a movie if the first week went well. But the first week's box office has to do with people who went because they liked the trailer. There's no information about the actual movie. And critics are no help. They either think their job is to criticize it, tell you if they liked it, or just tell you everything that could possibly be of interest in it. Their job is really to tell you enough about the movie so you can decide if you might like it or not, but not give so much away to ruin it. It's not an easy job, and few have succeeded. So we go to movies we don't like. In fact, one time, i went to the theater and watched the wrong movie. It turned out to be the better choice. And that's what i think about when we're talking about ants. Remember, there are way more ants than uncles.

Google Reader Goes Away

As you may know, Google Reader is set to disappear on July 1st. I (finally) transferred my subscriptions. It took longer than i expected, and transferred less than i'd hoped. Reader says you can export your date via Takeout. You get to save your stuff to your local hard disk. I downloaded everything, which gives you a .zip archive. I unzipped the zip (there's an unzip command line in Linux, but it's probably easy on any platform).

Historically, i ran Sage in Firefox as a reader. When Google Reader came around, I switched to it so that I could continue where i left off on multiple machines. With Google Reader gone, i've switched back. The directions found by searching the Internet yielded lots of false leads. What works is to bring up Firefox and Sage, in the options menu (on the left), import OPML, browse to the .xml file in the stuff you downloaded and unzipped. What you get is the subscriptions. It didn't have the stuff that's marked as read/unread, however.

Sage has changed since I last used it. It looks better. But it's still a basically simple blog reader. Since I really mainly use one machine, i think i'm going to like it better than Google Reader. For one, it either seemed impossible, or was impossible to mark something as unread that i might have started but didn't finish, or simply wanted to reread.

Sage shows the articles in the browser, just like they'd appear on the original blog. That's because you're looking at the original blog. Google Reader reformatted stuff. This was OK sometimes, but not always. And though you could click to see it in the original form, you had to do that in order to see if you were missing anything. Why not always look at the original? And, some blogs would make a big deal of how their work was copyrighted, and prohibited derivative work. Google Reader was clearly making a derivative work. And, this could hurt the original blog. That's because Google Reader didn't do any advertising for the original author - though they did do some for themselves.

How far can the Sun be seen?

How far away from the Sun can you just barely see the Sun (using Wikipedia)? The Sun is magnitude -26.74 (from Wikipedia). The dimmest stars one can see with the naked eye are approximately magnitude 6. The Sun would have to be |-26.74 - (6)| = 32.76 magnitudes dimmer. The formula for magnitudes is x^5 = 100, x = 100^(1/5), where x is the multiplier to get from one magnitude to the next. The factor dimmer that Sun must be is x^32.76=12,705,741,052,085 (more or less). Light gets dimmer with the square of the distance. Since the Sun is at one AU (x^32.76)^(1/2)=3,564,511 AU is the distance where you can just barely see the Sun. How far is that? 1 AU = 149,597,870,700 meters, exactly. 3,564,511 AU * 149,597,870,700 m/AU = 533,243,305,691,677,319 meters. 1 light-year = 9460730472580800 metres (exactly). 533,243,305,691,677,319 m / 9.4607×10^15 m/LY = 56.363861885414590497131460401964 light years. (OK, so that's more digits than we need). If you were 56.364 Light Years away, you'd be just barely able to see the Sun.

Garnet

Never saw the web magazine The Shallot before. Of particular note is the announcement of a new programming language: Garnet. This is the very first pure non-functional language. Garnet is related to Ruby, only not really.

Eight Queens part one

	Q
Q

If you get out a chess board, and put a queen in the lower left square, it's pretty clear that you can't put a second queen in the lowest row of the second column. That's the same row that the first queen is in. So there are really only seven choices available for the second queen. And the third queen only has six choices. It follows that there are 8 * 7 * 6 ... or 8! = 40,320 possible board positions to check for solutions. So combining the not-in-the-same-column rule with the not-in-the-same-row rule reduces the number of board positions to check by a factor of (8^8)/8! = 416.

There are algorithms that turn a counting integer into a unique permutation of a list. One could use this sort of thing. There are three reasons for not moving forward in this direction. First, the permutation algorithm is a bit complicated. It's nearly as long as the current program. Second, this permutation algorithm is fairly slow, though not anywhere near a factor of 416 slow. And its performance per call is proportional to the number of items to permute, in this case eight. Third, changing an exponential algorithm (8^8) into a factorial problem (8!) still gives you exponential time. If the board size is increased, the solution increases in time proportional to x^n of the board size. The permutation algorithm is handy. So perhaps it'll get a write up in some other series. This series has another direction. And if this code is converted to counting permutations, then it will be difficult or impossible to go where we're going.

		Q
	Q
	Q
Q	Q

Let's return to the chess board. Put the first queen in the lower left square. In the second column, you can't put a queen in the lowest square. If you put the second queen in the second row, then the two queens are also attacking each other, this time diagonally. In fact, with the second queen in either of these positions, there are no queen positions of the remaining six queens that are solutions to the Eight Queens problem. You may as well move the second column queen up one more square. If you skip checking the positions with the other six queens, you've skipped 2*8^6 = 524,288 positions (of 16 million). And, you've skipped all these board positions with a two checks. It's easy to show that if the first two queens are as shown, the third column queen must be at least at the fifth row. To get the third column queen that high, four more checks are made, eliminating 4*8^5 = 131,072 boards. Big chunks of the problem space are vanishing, though they're vanishing in smaller chunks as the queens farther to the right are placed and checked. But this is the general way that the student in 1979 came up with his nearly zero time solution. It's also what Dijkstra did in his 1972 article about Structured Programming. However, this article isn't about Structured Programming (that would be a completely different rant) so much as it's about the technique Dijkstra used called Backtracking.

To make use of Backtracking you need to be able to generate a first board, a next board (and know if there aren't any more), you need to be able to check the partial solution, and you need to be able to print or otherwise identify the solutions you found.

Let's see how it works. The first board routine needs to simply place the first queen. In the check board routine, there's only one queen, so there are no attacks. The next board code knows that there is a possible solution, so it puts a new queen on the board in the next column. From here on, it's only check board and next board. The check board function needs to know how many queens are on the board so it can check rows and diagonals for attacks. In this case there are two queens, and they're in the same row, attacking. The next board function needs to know if the check board found an attack or not. Since there's an attack, it needs to move the rightmost queen up a row. When it finds a queen is at the top already, then it is removed, and the previous queen needs to be moved up. This is Backtracking.

For the Eight Queens problem, the initial solution space was so large, that it seemed hopeless. But it turns out that Backtracking is an approach that can be used to attack many of these combinatorial problems. The downside for Backtracking seems to be that it isn't very easy to decide how good the performance will become without first trying it. In this case, as queens to the right of the board are considered, smaller chunks of the problem space are eliminated. With increasing board size, does the problem stay exponential? Or is it something else? Knuth wrote about this issue in 1975. From my perspective, it doesn't matter. That's because Knuth is primarily thinking about the problem as a mathematician. Mathematicians want to think about a problem and come up with a solution. Programmers have another tool. They can write yet another program and see how it works. If the program takes too long, the programmer can tell the computer to count something of interest to help the analysis. Often this shows the programmer where to attack the problem next.

Don't agree with me? Here's an analogy. My favorite sorting algorithm is Shell's Sort. How long it should take is an open question. One advantage that it has over other algorithms is that an in-place sort doesn't require extra memory. It usually performs similar to n*log(n). In practice, it's usually quicker than Quicksort which has a best case of n*log(n) time, but requires more space. It doesn't bother me that its computation time is an open question.

In any case, let's look at a modification to the 8^8 version of the Perl program that does Backtracking. It's instrumented to find out how many rows needed to be checked (which is the number of next boards, and the number of diagonals checked. One should note that the board checks are faster than the previous version. That's because instead of checking all eight queens against all eight queens, it only has to compare the most recent queen to other queens. The previous queens have already been checked, and none are attacking. Since only 15,720 boards were checked, that's less than one in a thousand compared to the 8^8 solution. Fewer than one in three thousand diagonals need be checked. What does that mean for the order of computation? Not much. This code is written for an 8x8 board. It could be generalized to nxn, and then run, and then we'd find out... something. Since the checks are proportional to the size of the board, we'd expect time to rise faster than board size. However, the chunks that would be eliminated would be a larger proportion for larger boards. So, who knows? I'd be willing to bet that someone has written this up somewhere.

#!/usr/bin/perl

# Eight queens - incremental backtracking version.
# Chess board where eight queens are not attacking each other.
# Can't have two queens in the same column, so represent row numbers in columns.
# There are 8^8 (1e7) positions to check.
# The check for one queen per row gives you unique digits.
# If there's an attack between queens to the left, there's no
# need to keep checking to the right.
# This reduces the problem further.
# 92 winning boards. 15720 rows checked, 5508 diags checked.
# 0 seconds - likely less than 0.05 seconds.

# main
my $col = 0; # current column under consideration
my $x;
my @b; # board, 0 - 7 are columns, values are positions, 0-7
my $cnt = 0;
my $chkh = 0; # horizontal checks
my $chkd = 0; # diagonal checks

# set board to queens at bottom.
for ($x = 0; $x < 8; $x++) {
 $b[$x] = 0;
}
while (1) { # The big loop, count to 8^8-1
 # check for a win
 if (&chkwin($col)) {
  if ($col != 7) {
   $col++; # Don't increment board, as new col is zero.
  } else {
   $cnt++;
#  print "win ";
   &prbrd();
   $col = &incbrd($col); # increment the board
   if ($col == -1) {
    print "$cnt winning boards.\n";
    exit(0);
   }
  }
 } else {
  $col = &incbrd($col); # Increment the board
  if ($col == -1) {
   print "$cnt winning boards. $chkh rows, $chkd diags.\n";
   exit(0);
  }
 }
}

sub incbrd { # Returns $col. -1 when done.
 my $col = shift;

 $b[$col]++;
 while ($b[$col] > 7) {
  if ($col != 0) {
   $b[$col] = 0;
   $col--;
   $b[$col]++;
  } else {
   return -1; # done
  }
 }
 return $col;
}

sub prbrd { # Print the board
 my $x;

 for ($x = 0; $x < 8; $x++) {
  print "$b[$x]";
 }
 print "\n";
 # sleep(1);
}

# Assumes partial incremental board.
# Only have to check the rightmost column.
sub chkwin {
 my $col = shift;
 my ($x, $y, $a);

 # Check for same row.
 $chkh++; # How many horizontal checks.
 for ($x = 0; $x < $col; $x++) {
  if ($b[$x] == $b[$col]) {
   return 0;
  }
 }
 # Check for diagonal.
 $chkd++; # How many diagonal checks.
 $a = 1;
 $y = $b[$col];
 for ($x = $col - 1; $x >= 0; $x--) {
  if (($y == $b[$x] - $a) ||
      ($y == $b[$x] + $a)) {
   return 0;
  }
  $a++;
 }
 return 1; # 1 is good, 0 is not a win.
}
0;

Could this code be made faster? Sure. For one thing, any solution that is up/down mirrored is also a solution. So the left most queen only needs to go from 1 through 4. The mirror solution can be created by subtracting the row number for each column from nine. So one becomes eight. It's an easy change. It would produce all the answers in a little over half the time. Perhaps tricks like that allowed someone to compute the number of distinct solutions for a 26x26 board. Time spent counting alone would take forever. One expects that they used a compiled language. That would improve performance by a factor of about three hundred. This code could be converted to C without changing much of the look. And it could be converted to run on multiple processors fairly easily.

The interested reader might note that the general algorithm for Backtracking is presented as recursive, and the Eight Queens code that Wirth presented is also recursive. My Perl solutions are not. My policy on recursion is to introduce it if it helps with dynamic storage. In this case, restoring the previous state is a simple matter of changing the value of the column under consideration ($col). A further issue is parallelization. Multiple core processors are now common. We should be considering parallel computations. It looks pretty easy to start with my code and modify it for multiple processors. For example, it could be modified to consider the case where the first queen is set once, and not moved. All of the other boards with this first queen would be considered. Eight instances would be run, possibly at the same time. Perhaps something similar could be done with a recursive version, but it may not be so easy. It's something for future investigation.

This code was timed with a resolution of one second. Why work hard to reduce a fifty second program you need to run once to nearly zero? The answer is that these techniques are worth learning. There are other problems where even modern machines are hopelessly slow. We'll get to one of those soon.

Eight Queens part zero

How many queens can be put on a chess board where none of them are attacking any others?

A chess board has eight by eight squares. A queen attacks all squares in the same row or the same column, or on either of the two diagonals.

If one considers putting queens on a chess board at random, the maximum number of board positions to consider is 64! That is, one puts a queen on the board, and there are 64 choices for where to put her. For the second position, there are only 63 open squares left. So for two queens, 64 * 63 positions need to be considered. There are 64 squares, so the maximum number of queens is 64. The number of positions to check is 64 * 63 * 62... or a total of 64!. That's about 10^89 positions. All the computers on Earth could not check that many board positions in the current age of the Universe. The overwhelming majority of these board positions can be shown to have at least two queens attacking each other. And there are some simple ideas to eliminate whole chunks of these at a time. For example, here's one idea.

Since a queen attacks all the squares in the same column, one can't have two queens in the same column. Since there are only eight columns on a chess board, it's not possible to have more than eight queens on a chess board without any attacking any others. It can be ruled out. That doesn't mean that there are any board positions with eight queens. It only means there aren't any with nine or more. This is apparently obvious enough that the problem is called the Eight Queens problem.

This not-in-the-same-column rule means that the queen in the first column can be in any of eight positions. For each of those, the queen in the second column can be in any of eight positions, for eight squared combinations. It follows that the total number of board positions to check is eight to the eigth power (8^8), or a bit over 16 million board positions. This is a speed increase over our original idea of a factor of about 10^81.

The Eight Queens problem, is an example of a combinatorial problem. It is said to be NP-complete. The solutions for these problems suggest that the entire solution space must be searched to find solutions. NP-complete problems strike fear in the hearts of computer science students. Having never been a computer science student, it's not much of a worry. However, my understanding of gravity is excellent, so acrophobia is available. It's always something.

While at school in 1979, i had a job sitting behind the I/O desk, answering student's computer questions. One day, an advanced computer science student asked me about the problem. The professor had likely read Dijkstra's 1972 article, and assigned it to a class. He prepared the class for the worst by implementing an 8^8 solution that attempted to get all solutions by brute force. After three days, it had covered a third of the solution space, and he killed it. The estimate was nine days for the full solution. This is on a PDP-10 designed in 1966 that performed at about a fifth of a MIPS.

Anyway, on a modern machine, 10^7 is not such a big number of things to do, so let's just plow into it. How should a computer program represent the board? It could have an eight by eight grid, with a one representing a queen, and a zero representing an open space. Since the numbers are either zero or one, the numbers don't have to be larger than one bit. 64 bits could be used.

A program with this representation needs code to generate a first board position, code to generate the next board position in any way that covers all possible board positions, code to check to see if a board position is a solution, and code to print or otherwise note a solution. One can imagine each of these routines. The first board position could be all eight queens at the bottoms of their columns. The next board position could move the rightmost queen up a row. But if that move the queen off the top of the board, it should move it down to the bottom of that column, and move the queen to the left up a row. When all the queens are at the top, it should report that all positions have been searched. The check for win must check each queen's row for other queens, and each queen's diagonals for other queens. A board position print might print a space where there are zeros and a queen where there are ones in an eight by eight square.

Here's another way to represent a board position. In each column, only one queen may be present. So each column can be represented by a single number. This number says what row that queen is in. There are only eight columns, so there are only eight numbers. Each column has eight rows. So each number can have one of eight values, so only three bits are needed. That's a total of 24 bits. In any case, you can think of each column as a digit in a number. As long as the digits are constrained to one of eight unique digits, you can count through all possible board positions. One of the nice features of this representation (compared with a bit per square) is that as you "count" through possible board positions, you don't have to check that two queens are in the same column. That is, the board representation can't violate this constraint, so there's no need to check.

The same routines are needed for the eight numbers as above. If each digit is one through eight, then the intial board could be all ones. The next board looks like counting by one. Checking for a queen in the same row is the same as checking the other queens for the same digit number. Checking diagonals is a bit more complicated. Two columns that are next to each other have a diagonal that are off by one row. If they're one row farther apart, then diagonals are two rows different. Finally, though a full board can be printed, it's easy enough to simply print the row numbers for each column.

This 8^8 Perl program takes 50 seconds to find all solutions. That's because a modern desktop machine is at least 15,000 times faster.

#!/usr/bin/perl
# Chess boards where 8 queens are not attacking each other.
# Can't have two queens in the same column.
# Represent row numbers in columns.
# There are 8^8 (1e7) positions to check.
# 50 seconds - 335544 board checks per second.

# main and global variables
my $col = 0; # current column under consideration
my $x;
my @b; # board, 0 - 7 are columns, values 0 - 7 are positions
my $cnt = 0;

# Set board to queens at bottom.
for ($x = 0; $x < 8; $x++) {
 $b[$x] = 0;
}
while (1) {
 if (&chkwin()) { # check for a win
  $cnt++;
  &prbrd();
 }
 if (&incbrd() == -1) { # increment the board
  print "Done $cnt winning boards.\n";
  exit(0);
 }
}

sub incbrd { # Increment board.
 my $col = 7;

 $b[$col]++;
 while ($b[$col] > 7) {
  if ($col != 0) {
   $b[$col] = 0;
   $col--;
   $b[$col]++;
  } else {
   return -1; # Puzzle is done
  }
 }
 return $col;
}

sub chkwin { # Check a board for a win.
 my ($x, $y, $a);

 for ($x = 0; $x < 8; $x++) { # Check row
  for ($y = $x + 1; $y < 8; $y++) {
   if ($b[$x] == $b[$y]) {
    return 0; # not win
   }
  }
 }
 for ($x = 0; $x < 8; $x++) { # Check diagonals
  $a = 1;
  for ($y = $x + 1; $y < 8; $y++) {
   if (($b[$y] - $a == $b[$x]) ||
       ($b[$y] + $a == $b[$x])) {
    return 0; # not win
   }
   $a++;
  }
 }
 return 1; # win
}

sub prbrd { # Show the board.
 my $x;

 for ($x = 0; $x < 8; $x++) {
  print "$b[$x]";
 }
 print "\n";
}
0;

The Eight Queens wiki page tells us that the first solutions were found in 1850, about 96 years before the first fully functional computer, depending on who you talk to, and what your definition of fully functional computer is. If any solutions can be found by hand, there must be better ways to approach this problem.

My help to the student was likely limited to some hand waving about reducing the problem space, without any real direction. A couple days later, he showed me that he'd reduced the time required to less than a second. He even removed the print statements showing that most of that time was spent printing the answers. There are only 92 of them.

In the next part, the problem is approached using a better technique. It may seem pointless, since the most time that can be saved is about fifty seconds. But the general technique can be used on many such problems. And many of these problems are considerably more complicated. It's best to practice on easier problems first.

Crimson

It was mostly clear last night. I thought it might be fun to see if i could find R Laporis, also called Hind's Crimson Star. Though visible from my back yard, which has better stray light blocking, it did not appear that i could get my telescope's computer aligned in a spot where i could see it. So, i brought the scope to the front sidewalk (the Mercury Vapor Observatory). The MVO has had a much wider sky view than the jungle in the back yard ever since the Emerald Ash Borer took down the front yard's twin gorgeous ash trees. I've never actually seen one of these beasts.

The constellation Lepus (the hare) is below the feet of Orion. This part of the sky looks entirely star free at first glance. 10x50 binoculars show the stars of the constellation easily. But after a few minutes, there seemed to be enough stars visible to the naked eye to sort of fill it in. At the MVO, there really isn't anything like dark adaptation for the eyes. It's more like scanning the area, paying attention, and using averted vision techniques to bring out the dimmer stars. I should note that the constellation looks more like LEPUS on the Orion wiki page than on the R Laporis wiki page.

The ten inch scope cooled down, and i performed an alignment using Rigel and Polaris. Rigel was chosen because it's near the target. Polaris was chosen because it was handy. The computer reports how good the alignment was, and it was excellent. R Laporis is less than a degree above NGC 1710. NGC 1710 is a galaxy that is absolutely invisible from the Mercury Vapor Observatory, since it's not one of the three brightest galaxies in the sky. The idea was to get into the neighborhood. It took about a minute of searching to find it. My wife also got a look at it briefly, before clouds blocked it. It looks like a seriously red LED light. Orion's Betelgeuse is also a red supergiant. And it's nearby in the sky, so i took a look at it for comparison. While Betelgeuse is somewhat orangish naked eye, it looked positively white in the scope, though not white like Rigel. The difference for R Laporis is that the star pushes carbon into its atmosphere. This carbon blocks blue light from the otherwise red giant, making it look much, much redder.

R Leporis is fairly faint, at about 10th magnitude. This is not a problem at the MVO. This ten inch (254 mm) scope has a collecting area (with the secondary mirror subtracted) of 47,553 square millimeters. My eyes dilate to 6.5 mm, which works out to 33 square millimeters. So the scope brings in 1,433 times more light into my eyes. That works out to a light grasp improvement of about 7.9 magnitudes. I was seeing 4th magnitude stars naked eye, so 12th magnitude should have been reachable with the scope. In addition to that, even low magnification (48x) tends to dim extended objects like galaxies and the sky glow, but not point like objects like stars. So the contrast is much, much better. A tenth magnitude star is fairly bright in the scope. Unfortunately, I didn't get a chance to see if R Laporis was visible in the 9x50 finder scope. It wasn't obvious in the 10x50 binoculars, but i didn't yet know exactly where to look.

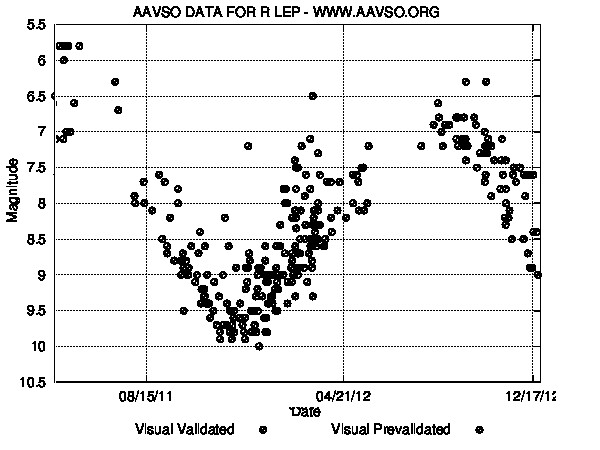R Laporis is a variable star with a period of about 432 days (14 months). It most recently peaked near magnitude 6 in November 2012. So it should be faintest in June 2013 near magnitude 11. Here's the current AAVSO light curve. To search for the star, use R LEP on the AAVSO web site. R Laporis should be at peak brightness again in January 2014 (about 40 times brighter). And, Orion, and therefore Lepus, will be well placed in the evening sky as well.

It was freezing cold, so i limited myself to a few other objects. Polaris and Rigel were alignment stars. Though i could have aligned using the finder scope's cross hairs, the main scope was used. Betelgeuse, Rigel and Sirius were used for comparison. Sirius was blinding. Jupiter was above the first quarter moon. The four Galilean moons were clearly visible in 10x50 binoculars. I didn't look at the Moon with optics, as the sky was very clear, and the moon filter was in the house.

Forth for Enlightenment, part thirteen of ten, Primes too

In part nine we had an introduction to testing if a number is prime. A function to check for primality was presented. It's short and to the point. And, since it checks by dividing the number by all integers up to the square root of the number, the execution time is proportional to the square root of the number. Is there something that can be done to speed it up? Absolutely.

For one thing, all numbers greater than two are divisible by two. So dividing by those numbers doesn't have to be done. One can test for even numbers by starting with three and skipping every other number. That's a quick and easy test. One can apply the same logic and skip numbers divisible by three after three. That's a little more complicated. The easiest approach appears to be to note that you can skip every other division by three, since those are divisible by two. That is, one can skip by six, and only check some of the numbers in each block. This code performs this sort of check. It searches two and three, then by sixes starting with five.

«
 0 0 → n s a «
  IF n 2 < THEN
   1 'a' STO
  ELSE
   IF n 3 > THEN
    IF n 2 MOD 0 == THEN
     2 'a' STO
    ELSE
     IF n 3 MOD 0 == THEN
      3 'a' STO
     ELSE
      IF n 7 > THEN
       n √ FLOOR 's' STO
       5 s FOR x
        IF n x MOD 0 == THEN
         x 'a' STO
         s 'x' STO
        END
        IF n x 2 + MOD 0 == THEN
         x 2 + 'a' STO
         s 'x' STO
        END 
       6 STEP
      END
     END
    END
   END
  END
  a
 »
» 'ISP2' STO

Here are some timings to show the speed up. On the left is the number that is tested. Then, the number of seconds for ISP and ISP2 to complete the check. Note that all numbers tested are, in fact, primes. So this is sort of the worst case. There was no run of 10000019 for ISP.

Number	ISP	ISP2
10007	5	2.3
100003	15	5.4
1000003	47.3	15.5
10000019	na	47.7

In any case, it's pretty clear that as the number goes up, so does the time. Of note is that ISP2 performs about as well as ISP does on numbers that are ten times larger. That's because both algorithms have time that goes up with the square root of the number. The ISP2 implementation is faster because instead of checking every number, it checks two numbers for every six. That's one third the number of divide checks. Since it does one third as much work, it should perform about as well on number 3 * 3 = 9 times larger. Nine is pretty similar to ten from a benchmark perspective.

This factor of three performance increase comes at a cost. For the HP-28c, this cost is size. While ISP only requires 82 bytes, ISP2 requires 443 bytes. Is that a big deal? Yes. For one thing, since this is a single big function, if you make a mistake and need to edit it, you get "No room to enter". You have to type the whole function in again from scratch.

Are there prime number test algorithms that do better than going up in time with the square root of the number? Yes. But they either require remembering stuff, or have more code, or both. The HP-28c simply doesn't have the memory to do a significant sieve or the code for the Miller-Rabin primality test.

Forth for Enlightenment, part twelve of ten, Four Digit Puzzle

This is another number based logic puzzle. It can be solved without a computer. It's not difficult. The mostly brute force coded solution is straight forward too. It's included because of the rewrites. Like the previous puzzle, individual digits need to be examined. An experiment for this code is to use strings to extract digits. First the problem statement.

What is the four digit number in which the first digit is one-third the second, the third is the sum of the first and second, and the last is three times the second?

First, just a minor bit of analysis. We're looking for a four digit number. One imagines that four digit numbers have a range from 1000 to 9999. I mean, what's the difference between 0000 and 00000? Is the later a five digit number? But 0000 is a solution, right? This program assumes 1000 to 9999, but to save time, it stops when it finds a solution. The code 9999 'X' STO sets the variable X to its final value, so that the FOR loop ends. Without this, the program takes well over an hour to execute, and finds only the one solution.

«
 1000 9999 FOR X
  X →STR 1 1 SUB STR→ 'A' STO
  X →STR 2 2 SUB STR→ 'B' STO
  X →STR 3 3 SUB STR→ 'C' STO
  X →STR 4 4 SUB STR→ 'D' STO
  IF A 3 * B ==
   A B + C == AND
   B 3 * D == AND THEN
   X
   9999 'X' STO
  END
 NEXT
 'A' PURGE 'B' PURGE 'C' PURGE 'D' PURGE
 440 .1 BEEP
» 'PUZ4' STO

This code requires 307 bytes of memory, and takes and 225 seconds for execution. It produces the right answer, 1349.

So, X →STR takes the number X, and converts it to a string. 1 1 SUB returns the substring that is the first character. Since more arithmetic needs to be done, STR→ converts it back to a number. Once each digit is isolated, it is assigned to a global variable. The number, X or ABCD, is a candidate solution. The IF statement figures out if ABCD is a solution or not.

The IF statement performs each of the tests. A 3 * B == multiplies A * 3, and compares it to B. A has to be an integer from 0 to 9. And so does B. One can multiply A by 3 or divide B by 3 and get the same result. The next bit, A B + C == AND adds A and B and compares the result to C. The AND bit combines the first two logic results. The result of the AND is true only if both of the conditions are true. Finally, B 3 * D == AND multiplies the second digit by 3 and compares that to the 4th digit. AND combines the result with the first two results.

The code 440 .1 BEEP makes the machine beep at the end. That makes it easier to time the execution with a stopwatch.

The next idea explored is saving X →STR on the stack, instead of recalling X and converting it to a string 4 times. The code X DUP DUP2 puts 4 copies of X converted to a string onto the stack. One copy is consumed in each of the following lines.

«
 1000 9999 FOR X
  X →STR DUP DUP2
  1 1 SUB STR→ 'A' STO
  2 2 SUB STR→ 'B' STO
  3 3 SUB STR→ 'C' STO
  4 4 SUB STR→ 'D' STO
  IF A 3 * B ==
   A B + C == AND
   B 3 * D == AND THEN
   X
   9999 'X' STO
  END
 NEXT
 'A' PURGE 'B' PURGE 'C' PURGE 'D' PURGE
 440 .1 BEEP
» 'PUZ4' STO

This version is smaller, using only 291 bytes. It's also faster, taking 190 seconds.

Using strings to extract digits was an experiment. We had a numeric digit extractor called G in our previous number puzzle. Here it is.

«
 DUP 10 / FLOOR SWAP 10 MOD 
» 'G' STO

The G function takes a number, and produces the number divided by ten, and the remainder. This peels off the least significant digit. So the right most digit, D is obtained first. G is then called with the new smaller number to peel off the next digit. It doesn't get called for the last digit, since we know that the number had four digits. The third call to G must produce the first two digits. The program that uses it looks like this:

«
 1000 9999 FOR X
  X G 'D' STO
  G 'C' STO
  G 'B' STO
  'A' STO
  IF A 3 * B ==
   A B + C == AND
   B 3 * D == AND THEN
   X
   9999 'X' STO
  END
 NEXT
 'A' PURGE 'B' PURGE 'C' PURGE 'D' PURGE
 440 .1 BEEP
» 'PUZ4' STO

It's slightly bigger than our optimized string version at 306 bytes of memory. But it's faster, taking only 103 seconds. The substring idea looked like it might be quicker, but it wasn't.

One thing of note is the PURGE commands towards the end. Global variables are convenient, but they've got to be cleaned up at the end, otherwise, they stay around for the user to clean up. This isn't much of a big deal on the HP-28c, but on the HP-28s, there's much more memory, and more than one program might be loaded at a time. These variables would add clutter everywhere. Local variables get cleaned up automatically. And we learned how to use them in a recent post. However, we need to change the G function to produce the digits on the stack all at once. That is, it leaves the shortened number on the stack where it can be used to produce the next digit. All the digits produced stay on the stack until converted to local variables.

«
 DUP 10 MOD SWAP 10 / FLOOR
» 'G' STO

Then the program follows.

«
 1000 9999 FOR X
  X G G G 
  → D C B A «
   IF A 3 * B ==
    A B + C == AND
    B 3 * D == AND THEN
    X
    9999 'X' STO
   END
  »
 NEXT
 440 .1 BEEP
» 'PUZ4' STO

This local variable version is shorter, using 266 bytes and faster, taking 69 seconds. I'd have thought this version would be slower, since variables are created and destroyed every loop. So, not only is this version smaller and faster, but it looks easier to read to me.

The code → D C B A « takes the four digits that are on the stack, assigns them to local variables D, C, B and A. Local variable blocks can go anywhere.

Curiously, in RPL, variables of any kind must be given an initial value. It's impossible to have a variable that isn't initialized. Using a variable that doesn't yet have a value is simply not a bug you can code in this language. Fortunately, there are lots of other kinds of bugs you can code, more than making up for this deficiency.

The next idea is to try nested IF statements. Nested IFs are logically the same as the AND statements. They should be quicker since the tests can stop as soon as one is false. The C language allows shortcut logicals where additional conditionals are not evaluated. RPL on the HP-28c does not.

«
 1000 9999 FOR X
  X G G G 
  → D C B A «
   IF A 3 * B == THEN
    IF A B + C == THEN
     IF B 3 * D == THEN
      X
      9999 'X' STO
     END
    END
   END
  »
 NEXT
 440 .1 BEEP
» 'PUZ4' STO

This version is larger at 296 bytes, but it's also faster at 54 seconds. Is it easier to read? Experimentation with the order of the IF statements did not yield a change in speed. One might expect that putting the condition that is false most often first would be faster, as less code is executed on average.

Finally, we'll inline the G function. The HP-28c's RPL encourages using and calling functions, but it takes time to call a function and return. The resulting code is bigger since the G function is 49 bytes by itself, and this version has three copies of it. It's not necessarily easier to read, but it is quicker.

«
 1000 9999 FOR X
  X
  DUP 10 MOD SWAP 10 / FLOOR
  DUP 10 MOD SWAP 10 / FLOOR
  DUP 10 MOD SWAP 10 / FLOOR
  → D C B A «
   IF A 3 * B == THEN
    IF A B + C == THEN
     IF B 3 * D == THEN
      X
      9999 'X' STO
     END
    END
   END
  »
 NEXT
 440 .1 BEEP
» 'PUZ4' STO

This version requires 334 bytes, but comes in at 47 seconds. That's about 4.8 times faster than the first version. Is that as fast as it can be done? Of course not. For one thing, the problem can be solved without a program, and it doesn't take very long. This exercise is about optimization. In this case, we didn't know the relative speeds of different functions before we started. So, a black box trial and error system was used to deduce what turns out to be fast or small. For RPL, this is what it takes. But it often takes something like it in other languages. You might think that instruction speed in assembly language would be well known. But most modern processors sometimes can perform instructions while waiting on external memory, or can even execute multiple instructions simultaneously. And often, one needs to sign a non-disclosure form to get the documentation. If that's not enough, various levels of cache miss or TLB thrashing can toss your best estimates out the window. Trial and error has the advantage of trial, which is sort of a final arbiter anyway. So make your best guess, and ask the universe if you're right.

Forth for Enlightenment, part eleven of ten, Number Problem Nine

I came across this logic problem. It uses numbers. I was able to solve it without the aid of any kind of computer. And there are computers that are way faster, and easier to use than my 1986 vintage HP-28c programmable calculator. But it looked as if a program to solve this just might fit on the beast, if barely. Also, it looked as if the run time to reach a solution might be less than hours. This machine isn't speedy. The processor has a cycle time of 640 KHz. Modern desktop processors are measured in GHz. There are 1000 KHz per MHz, and a 1000 GHz per MHz. Call it a challenge.

The following multiplication example uses all the digits from 0 to 9 once and once only (not counting the intermediate steps). Finish the problem. One digit has been filled in to get you started.

abc * d5 = efghi

Before we get started on the RPL program, let's do some minor analysis of the problem. The least significant digit produced by the 5 and c must either be 0 or 5. But if it's 5, then it's a duplicated digit. So digit "i" must be 0. That means that 'c' must be even. In fact, this program uses 'E' for Even instead of 'c'. The program doesn't have to guess either the 5 or the 0. Instead of a ten digit problem, it's an 8 digit problem.

ABE * D5 = STUV0

The program could cycle from 0 to 99999999. However, an empty loop that long takes about 8.8 days to execute. Since digits are non-repeating, and 0 isn't needed, the loop can start ABEDSTUV from 12346789 and go through 98764321. That brings it down to 7.6 days. The permutations of 8 digits that can only hold 8 distinct values is 8! = 40320. That's a loop that takes five minutes. But even there, it really only has to generate the permutations of the digits A, B, E and D from 1 through 9 excluding 5, multiply ABE * D5 and check to see if STUV also avoids 0, 5 and any of the digits A, B, E and D. And that's how this program does it.

Before you enter the program, you should know that i made numerous mistakes entering it into the machine. My first attempt had one huge function. When i finished entering it, i got "NO ROOM TO ENTER". This was on an empty HP-28c. It probably would have worked on an HP-28s, with its much larger RAM. But the HP-28c only has 2 KB of RAM, and only about 1700 bytes available when empty. It has to remember the whole function while compiling it into its internal form. This is effectively a show stopper for large functions. This version has two fairly large functions. Even here, when there's a mistake, you have to delete all the little functions to be able to edit either of the larger functions. So check your work. There's 498 bytes free on the HP28c after the run. This is one of the largest programs that can run on the HP-28c.

It would be nice to generate the permutations of ABED where A, B, and D can be 1, 2, 3, 4, 6, 7, 8, 9 and E can be 2, 4, 6, 8. But can it be done in a compact way? This program effectively counts digits, and skips inner loops when it comes to a digit that doesn't work. That leaves 8 * 8 * 4 * 8 = 2048 loops. This is well within the time constraints of the HP-28c. This program produces the correct answer 396 * 45 = 17820 in 270 seconds (four and a half minutes) and 800 seconds to search the entire problem space.

When i broke up the original function, i discovered that i needed global variables to get A, B, E and D into the inner loop. I considered passing them to the inner loop function as local variables, but then the helper functions couldn't access them. It's unfortunate in this case that the FOR loops create local variables, and helper functions can't access them. That's just the way it is.

This first function is the one you run when you've got everything entered. It doesn't take any arguments.

Check out the "2 8 FOR E" bit. The matching "2 STEP" makes it go from 2 to 4 to 6 to 8. In BASIC, the loop would be "FOR E=2 TO 8 STEP 2". The RPL version puts the STEP bit in a place that's not that easy to locate.

«
 1 9 FOR A
  A 'GA' STO
  IF A 5 ≠ THEN
   1 9 FOR B
    B 'GB' STO
    IF B CA THEN
     2 8 FOR E
      E 'GE' STO
      IF E CB THEN
       1 9 FOR D
        D 'GD' STO
        IF D CE THEN
         A 10 * B + 10 * E +
         D 10 * 5 +
         * 10 / LP
        END
       NEXT
      END
     2 STEP
    END
   NEXT
  END
 NEXT
» 'P9' STO

Then there's LP, the "loop part". It has one parameter, X. X is what you get when you multiply ABE * D5. X is then disassembled into STUV, with the 0 discarded. The G function does this disassembly. The argument is assigned to X using the right arrow (shift U on the HP-28c). This creates the local variable X.

«
 → X «
  IF X 999 > THEN
   X G 'V' STO
   G 'U' STO
   G 'T' STO
   G 'S' STO
   IF S CD THEN
    IF T CS THEN
     IF U CT THEN
      IF V CU THEN
       GA 10 * GB + 10 * GE + -> STR
       "*" + GD 10 * 5 + ->STR +
       "=" + X 10 * ->STR + "0" +
       DUP 0 DISP
      END
     END
    END
   END
  END
 »
» 'LP' STO

G gets the next least significant digit from a number. It's really divmod. It takes a number, divides it by ten, and gets both the quotient and the remainder. It returns both on the stack. This little ditty takes 49 bytes.

«
 DUP 10 / FLOOR SWAP 10 MOD 
» 'G' STO

Next come the helper functions that check to see if the given digit matches other digits. They return false (0) if any matches are found. Otherwise true. We could have a single function that checks all digits against all other digits. But it's better to check a single digit against what has been computed so far. That way, fewer total checks need to be done. The way this program achieves this is to cascade checks. The first function, CA, checks if the given digit matches A, the digit 0, or the digit 5. CB checks for a match of B, but then calls CA to check those. And so on, through CU, which checks against U, but then calls CT, which calls CS, and so on, calling all the functions to check all the digits. Checking E for 0 and 5 isn't needed, but it's done anyway, since that's done in CA. It's more or less harmless.

«
 DUP GA ≠ SWAP DUP 5 ≠ SWAP 0 ≠ AND AND
» 'CA' STO

These helper functions could have used IF/THEN, returning when false. This might be faster, but the code is bigger. The example below is not only much bigger (100 bytes vs 48 bytes), but it's slower on random input.

«
 IF DUP GA ≠ THEN
  IF DUP 5 ≠ THEN
   0 ≠
  ELSE
   DROP
   0
  END
 ELSE
  DROP
  0
 END
» 'CA' STO

CB checks the argument for ≠ B, then calls CA for A, 5, & 0.

«
 DUP GB ≠ SWAP CA AND
» 'CB' STO

CE checks the argument for ≠ E, then does CB. E stands for even, since this digit must be even.

«
 DUP GE ≠ SWAP CB AND
» 'CE' STO

CD checks the argument for D, then does CE.

«
 DUP GD ≠ SWAP CE AND
» 'CD' STO

CS checks the argument for S, then does CD.

«
 DUP S ≠ SWAP CD AND
» 'CS' STO

CT checks T, then does CS.

«
 DUP T ≠ SWAP CS AND
» 'CT' STO

CU checks U, then calls CT, which calls everything else.

«
 DUP U ≠ SWAP CT AND
» 'CU' STO

I liked this cascade style. It may not be the fastest (function calls are relatively expensive on the HP-28c, even though they're encouraged). It may not even be the smallest code. But it does work the way mathematicians think. That is, problems are attacked by solving small problems, then attacking a larger problems using the solutions to smaller problems that have already been solved. Languages like RPL and Forth have this in common with Lisp and variants like Scheme. One can design code this way for nearly any computer language. But i'm still a C and assembly language programmer at heart. I still like to shave off an instruction here and there which saves a few bytes (even if billions are available) and often a few nanoseconds or less. It should be noted that modern C compilers can do automatic function inlining. They can even note that a function can only possibly be called from one place, and not leave a callable copy. Using lots of little functions can still make such programs easier to maintain, without any penalties. In my experience, such techniques aren't limited to math and logic problems such as the above.

However, it's good to remember that superior algorithms often lead to the smallest, fastest code, and often by a large margin. For this test, one idea is to have an array of bits, one for each digit. Set the bits for 0 and 5. Then when each new digit is encountered, check if the new digit's bit is set, and if it isn't, set it. One routine clears the bits, and another does the check and set. I didn't code, test or time this idea.

That's all there is to it. Leave a comment if you manage to get it to work. Leave a comment if you attempted to get it to work and couldn't. Leave a comment if you improved it. The HP-28c is an ancient machine. But from time to time, i still see evidence that there are people who have one of these beasts. Maybe you have a younger model, like an HP-28s or an HP-48s. These programs should work with any of them.

Forth for Enlightenment, part ten of ten, local variables and loop exit

If you've been following this blog for a while, then you'll recall that i described a series of programs for a 1986 calculator, the HP-28c. There aren't any forward links in the series, though you can follow them easily enough in the blog's automatically generated links on the right side. They're more or less all together. Until now. I've decided to revisit the calculator, the language, and the descriptions.
Now that i think of it, there's an easy way to get access to all the previous articles in this series. Ten parts were planned, and labeled here zero through nine. Here are the links.
zero Count
one Factorial
two Logic problem pt 0
three Logic problem pt 1
four GCD
five Backwords pt 0
six Backwords pt 1
seven Backwords pt 2
eight Backwords pt 3
nine Primes
There are two features of the RPL language as implemented on the HP-28c that i really wanted, but didn't seem to be include. One is local variables. It turns out that RPL has local variables. And, they're documented in the manual. Worse, i'd written programs when the calculator was much younger that used them. There are a couple pages in the manual that describe it. Unfortunately, there aren't any examples of how to use them, but a little experimentation shows how they work. Above the "U" key, there's a right arrow. It's an operator that takes arguments to its left and right. To the right, you give it the new variable names. This list ends when a new block "«"(as a single character) is encountered. For each of the variables, that number of arguments are taken off the stack (to the left). A function with a local variable might look like this.

«
 1 2 → a b «
  a b 2 * +
 »
» 'FNAB' STO

This assigns 1 to 'a', 2 to 'b', recalls 'b' (2), multiplies it by 2, and adds 'a' (1). So 5 ends up on the stack. At the close of the block '«', the variables 'a' and 'b' vanish. You can assign new values to 'a' and 'b' at will in your program using 'STO'. Unfortunately, 'STO+' doesn't work with local variables. No idea why not. One can create a function that takes arguments on the stack, and has local variables like this:

«
 1 2 → a b c d «
  a b 2 * + c 3 * + d 4 * +
 «
« 'FNABCD' STO

This assigns two arguments from the stack to 'b', then 'a', then assigns 1 to 'c', and 2 to 'd'. So, if you call this function using 7 8 FNABCD, you get 'a' set to 7, 'b' set to 8, with an answer of 35.
The other feature that i'd like is some way to exit a loop early. The manuals extol the advantages of not having a functional GO TO. In my humble opinion, RPL (and Forth and Lisp) are not that easy to read. Perhaps GO TO would make it impossible. Or perhaps we should consider these read only languages. It is very likely that implementing an abusable GO TO would slow down these languages. And yet, it's common that you need to search a list for something, and you'd like to be able to stop searching when you've found it. You can use a WHILE loop, since there's a condition you can use to exit. But what do you do with a FOR loop? After all, the FOR loop creates a local variable, which gets automatically cleaned up when you're done with it. It's handy. Well, here's how you do it. You set the loop variable to the end value. This code puts A on the stack each loop. Run it, and 1 2 3 4 5 are on the stack. The number 6 doesn't go on the stack because when A is 5, it gets set to 10. The IF statement needs to be placed just before the NEXT. You can't use it to magically exit the loop from somewhere in the middle.

«
 1 10 FOR A
  A
  IF A 5 == THEN
   10 'A' STO
  END
 NEXT
« 'E' STO

The HP-28c has a printer, which prints to thermal paper. One way to save a program is to print it to the printer, then xerox the output. What happens is that the thermal paper fades with time. Making a copy can give you a high contrast print for longer. One thing that would be better is if you could print your program, but have another computer capture the output and store it to disk. Then you could make a CD, which would last quite a long time. However, the HP-28c has several non-ascii (non-standard) characters. You'd have to make sure that you also documented these. It turns out that the protocol that the HP-28c uses to talk to the printer is pretty straight forward. So building an IR receiver and capturing the data isn't that hard. I haven't done it yet. And this still leaves getting a program back into the calculator. The HP-28c does not have any kind of network input. The printer only accepts input. The HP-28c only emits output. If there's no printer, or it misses something or falls behind, well, too bad. And, i've discovered that you don't really know how to enter a program until you've entered it and made it work. So, once you have your killer application written, you need to copy it somewhere, delete it, and enter it from your notes. There's no way around this. Doing it sooner (when you still know the program) has the advantage that if you make a mistake, you probably still know enough about it to fix it. Doing it later than sooner has the advantage that if you can do it then, it's more likely anyone can.

What works in education - round up at Smithsonian

The Smithsonian has a series of articles on Finnish education. It starts by comparing Finnish education to 9/11. Really, it came without any apparent warning. I don't see much additional connection.

The meat of the series talks about why Finnish schools work despite costing 30% less than schools in the US. There are lots of reasons. No standardized tests means more time teaching students how to think. Did anyone think that teaching students how to take tests is a useful life skill? But there are surprises in the article. Some can also be read here at Business Insider, of all places.

Do (did) you like homework? I did. I work better when it's quiet. I can learn by reading a book. It's not harder for me than having someone else teach. So i got more done, more thoroughly and quicker at home. I expect that my experience is not the norm. My son's 4th grade teacher sent out math problems that most adults couldn't solve. Things like, "What is the sum of the integers from one thorugh one hundred?" Hey, i know that one: (100 * 101) / 2 = 5,050. Don't need a calculator, since 100 / 2 = 50, and 50 * 101 is easy. But WTF? Most adults can't do this without adding 99 numbers. Is homework good? Maybe - in moderation. Here's what the Smithsonian had to say.

My son went to a Montessori school from preschool through grade 5. But unlike this article, he managed to learn a technique for addition that resulted in the wrong answer 2 out of 3 times. You may have used a similar technique. To add 4 + 5..., you start with one number, say 4, on your fingers, and you add 5 fingers to it. Instead of correcting the mistake, i decided to make a complete break from it, and taught him addition and subtraction on an abacus. His math improved dramatically in a couple months. Regular readers of this blog will know that i'm not shy about using fingers for math. But it wasn't the school who taught it, despite the Montessori roots. I believe that's because the school didn't carry the method long enough. It wasn't a private school, but rather a charter school. That means that they got students pulled away from the public schools. These are students who have at least one parent who could fill out a 17 page application, and who actually did it. This is a big advantage for these students. The school doesn't have anywhere near the issues that public schools have. And yet, i also pushed my kid through to reading for enjoyment. I'm not against the Montessori method. But i don't like the way it's getting used here in the states very much. You can't talk about education seriously without Montessori.

My first thought was that all this guy wants to do is scientifically document stuff that good teachers already know. I mean, if you've got kids in front of you, then it's obvious. But he also wants more, and he gets what the serious issues are. He's got more to say here.

And yet, there is good stuff happening right here in the US. Salman Khan is doing good work, for example.

And, you've got to know what the Flynn effect is. My grandfather was an engineer. He'd have scored ridiculously good on modern IQ tests.

Bowling a Perfect Game

The gang at work did a team build thing. We went to a local bowling alley to shoot the breeze, eat pizza, and bowl a few games. I'd sprained my right wrist earlier in the month, and it was still a bit sore. I've bowled left handed in the past, but it's pretty dismal. Still, this is team building, not a real competition. My strategy was to try it right handed, and if it got too painful, i'd switch hands. The expectation was that each game would get worse. The sprain is by the pinky. The result was that i have no aim. It was sort of random, like Brownian pool. However, my scores were 85, 95, and 124.

The high point of the first game was that in frame six, i was tied for last place. That was the only time during the game that i wasn't alone in last place. In the ninth frame of the second game, i'd achieved 75. To equal my first game, i'd need to score 10. The only way to achieve that would be to bowl a spare and a gutter ball. See if you can figure out how i managed twenty in the tenth frame. That last game wasn't really better than the first two, except for three spares in a row, followed by a strike. I plugged the game scores into a spread sheet, and added a quadratic curve fitting trend line. The line goes right through the actual scores. It shows that by game six, i'm bowling 300 - a perfect game. Clearly, i should have played three more games. The math doesn't lie!

Curiously, the wrist felt much, much better (not worse) the next day. Who'd have guessed that?